All'interno delle ricerche di computabilità non-standard, gli iLabs hanno sviluppato un automa cellulare in 2 e 3 dimensioni basato rispettivamente su celle a forma di esagono e di dodecaedro rombico. Questo sito si configura non solo come un "contenitore di materiali", ma piuttosto come un "contenitore di idee", in cui attivamente presentiamo il nostro lavoro ed invitiamo ogni persona interessata a provarlo in prima persona e partecipare al dibattito filosofico e scientifico che ne scaturisce.
La sezione tutorial è un'introduzione agli automi cellulari, pensata per avvicinare - attraverso parole, immagini, simulazioni - anche il lettore inesperto ai nostri temi di ricerca. Accanto alle nozioni fondamentali, il tutorial introduce le peculiarità dell'approccio iLabs, le motivazioni e gli ambiziosi obiettivi a lungo termine del progetto.
L'applet 2D interattiva e la galleria di simulazioni 3D ci portano nel vivo della Matematica dei Modelli di Riferimento. L'automa cellulare a base esagonale - utilizzabile direttamente nel browser (per problemi tecnici con l'applet, consultate l'apposita sezione) - permette di esplorare in tempo reale il nostro modello di universo, apprenderne la caratterische più tecniche (come la rappresentazione degli operatori booleani) e visualizzare pattern interessanti. La documentazione di riferimento espone la regola utilizzata dall'AC, ne introduce le basi concettuali e commenta i dettagli dell'implementazione utilizzata - il codice è inoltre disponibile per il download e l'utilizzo offline con funzioni aggiuntive e prestazioni ottimizzate. La galleria 3D raccoglie alcune simulazioni effettuate sulla versione a dodecaedri rombici del nostro universo: è su tale versione che i nostri sforzi di "fisica della computazione" si stanno ora rivolgendo, nel tentativo di collegare la geometria generata dallo spostamento delle informazioni con generalizzazioni fisiche interessanti e testabili.
Le sezioni Esplora e Info di questo sito contengono ulteriore materiale di background per iniziare a sperimentare la matematica dei MdR. Infine, è disponibile una lista di FAQ ed un indirizzo mail dedicato per segnalazioni (scientifiche e non), domande e approfondimenti.
La versione inglese del libro è pubblicata nella collana Texts in Computing (College Publications, Londra).
Buon divertimento!
| La Matematica dei Modelli di Riferimento - 2D | La Matematica dei Modelli di Riferimento - 3D | 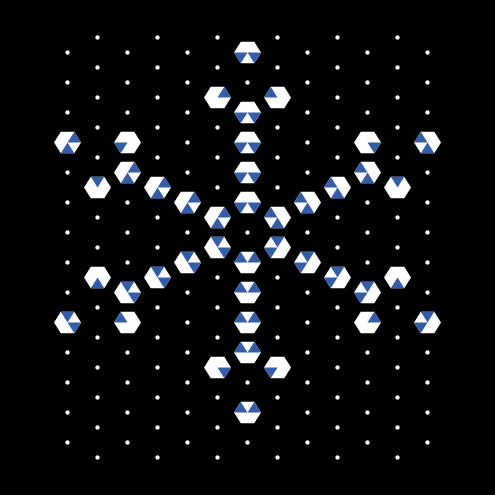 |

|
|---|---|
Vai alla simulazione 2D |
Vai alla galleria 3D |
| TUTORIAL | torna al top |
|---|
I. Cosa è un automa cellulare?
II. Perchè studiarli?
III. Quattro lezioni dagli automi cellulari
IV. L'AC iLabs: un'introduzione alle peculiarità dell'approccio
IV.I. E se la "Teoria del Tutto" fosse un AC?
IV.II. Spazio
IV.III. Tempo
IV.IV. Stati e regole
IV.V. Pensare è essere: è questa la soluzione?
V. Per saperne di più
| I. Cosa è un automa cellulare? | torna all'indice |
|---|
La teoria degli automi cellulari trova le sue radici nel lavoro di logici, matematici, informatici e fisici del calibro di Alan Turing, John von Neumann, Stanislaw Ulam, John Conway, Stephen Wolfram e Konrad Zuse. Gli automi cellulari (AC) sono rappresentazioni matematiche di sistemi complessi. Tecnicamente, un sistema complesso è un sistema dinamico - ovvero un sistema che evolve nel tempo e spesso in risposta all'ambiente - le cui proprietà sono determinate dall'interazione reciproca tra tutte le parti che lo compongono: una cellula vegetale, il corpo umano, l'economia italiana sono esempi di sistemi complessi, i quali, proprio in virtù delle intricate relazioni di causa-effetto tra i propri componenti, hanno comportamenti molto difficili da prevedere con precisione. Tipicamente, il marchio di fabbrica degli AC è la loro natura discreta sia nello spazio che nel tempo. Infatti, ogni automa cellulare presenta le seguenti cinque caratteristiche:
* Un reticolo discreto di celle od atomi; questo reticolo può essere a una, due, tre o anche a più di tre dimensioni. Le celle-atomi sono un po’ i “mattoni di base” dell’universo in cui l’AC consiste
* Un requisito di omogeneità: le celle devono erssere equivalenti in un senso preciso
* Stati discreti: ogni cella può assumere uno di un numero finito di stati discreti possibili
* Interazioni locali: ogni cella interagisce soltanto con un numero finito di celle che si trovano nei suoi dintorni, dette il suo vicinato o neighbourhood
* Dinamica deterministica: ad ogni istante di tempo, ogni cella aggiorna il proprio stato sulla base di una regola di transizione implementata nella cella stessa, che può essere la medesima per tutte le celle dell’AC, o diversa per celle diverse. Lo stato di una cella ad un tempo dato dipende sempre da quello (della cella stessa e) del suo vicinato ad un tempo precedente.
| II. Perchè studiarli? | torna all'indice |
|---|
Nel volume Cellular Automata: A Discrete Universe, Andrew Ilachinski elenca quattro motivi fondamentali per occuparsi di AC, in ordine crescente di importanza teoretica:
* Gli AC sono potenti sistemi computazionali
* Gli AC sono simulatori discreti di sistemi dinamici
* Gli AC sono strumenti concettuali per studiare la nozione di complessità e la formazione di pattern
* Gli AC sono modelli fondazionali della realtà fisica in se stessa
A partire dai pochi ingredienti di base listati sopra, infatti, gli AC sono in grado di modellare un’impressionante varietà di fenomeni e sistemi dinamici di grande complessità: dal movimento degli atomi di un gas nello spazio, a un circuito integrato, a una rete neurale, a un sistema dinamico molecolare, alla formazione di cristalli, allo sviluppo di una specie animale in una nicchia ecologica, a uno scontro militare.
Gli AC sono un elemento importante della nuova teoria della complessità, un programma di ricerca coltivato in centri quali il Santa Fe Institute in New Mexico. L’idea filosofica di base è che i fenomeni complessi siano un fatto emergente: il risultato della dinamica collettiva di un gran numero di celle-parti individuali piccole e semplici, che istanziano un ridotto numero di stati e si evolvono secondo regole semplici e meccaniche. Su macro-scala, un AC può far emergere pattern e strutture complesse che non hanno correlazione immediata con i semplici avvenimenti al micro-livello. Il più complesso sistema complesso a noi noto, l’intelligenza, è una proprietà emergente della più interessante porzione di materia a noi nota, il cervello umano – in cui miliardi di “celle-atomi”, i neuroni, istanziano e trasmettono informazioni sulla base di semplici meccanismi elettrochimici.
| III. Quattro lezioni dagli automi cellulari | torna all'indice |
|---|
Per farci un’idea più precisa del mondo degli automi cellulari possiamo considerare un esempio tipico di AC. Forse l’AC più conosciuto anche al di fuori del mondo degli specialisti è “Il gioco della vita” (the game of life), inventato dal matematico John H. Conway e reso popolare da Martin Gardner su Scientific American negli anni ’70.
Al di là dei singoli aspetti di modellazione scientifica più o meno specifica, gli automi cellulari si configurano come una "palestra di intuizioni" formidabile in cui mettere alla prova la nostra metafisica ingenua e molte delle più radicate convinzioni sulla struttura della realtà - convinzione che spesso, inconsciamente, finiscono per inquinare anche le nostre teorie più astratte:
* Lezione numero 1 → Non occorrono meccanismi complessi per generare complessità: regole semplicissime possono generare comportamenti inaspettati ed imprevedibili.
* Lezione numero 2 → Entità istantanee possono generare oggetti "persistenti": nonostante nulla, in un AC, duri più di un battito di ciglia, l'impressione è che alcuni oggetti (come gli "alianti" di Life), si spostino in modo uniforme nell'universo - se ci pensiamo, la stessa illusione che abbiamo quando i protagonisti di un film si "muovono" sul nostro schermo fatto di pixel.
* Lezione numero 3 → Un movimento discreto può ben approssimare un movimento continuo: la fluidità con cui gli alianti percorrono lo spazio rende il movimento qualitativamente indistinguibile rispetto ai movimenti che esperiamo quotidianamente, come quando lanciamo una palla da baseball. Questo suggerisce che la continuità dello spazio-tempo possa in realtà essere illusoria, e che tutta la realtà fisica sia un "grande automa cellulare" - o, in una ipotesi meno estrema, che anche se il mondo fosse fondamentalmente continuo, modelli discreti come gli AC possono essere comunque molto utili nel suo studio.
* Lezione numero 4 → Diverse "interpretazioni" della realtà sono possibili e ugualmente valide a priori: anche se il mondo di Life è fatto, in ultima analisi, solo di quadrati bianchi e neri, è possibile interpretare quello che accade a livelli diversi e in modi sempre nuovi; ad esempio, quello che possiamo descrivere come un aliante che si distrugge contro un blocco può essere visto anche come un microanimale che ne ingloba un altro. Entrambe le descrizioni, seppur incompatibili tra di loro, sono però metafisicamente sullo stesso piano: non dobbiamo dimenticarci che, per quanto ne sappiamo, anche il nostro mondo - fatto di quelle che chiamiamo "persone", "piante", "strade" - potrebbe avere uguale carattere convenzionale.
| IV. L'AC iLabs: un'introduzione alle peculiarità dell'approccio | torna all'indice |
|---|
Noi di iLabs non riteniamo che gli automi cellulari siano "solo" interessanti rappresentazioni o modelli astratti che approssimano fenomeni reali. Piuttosto, riteniamo che la realtà stessa sia proprio un grande Automa Cellulare! La nostra scommessa è che l’universo sia discreto, e anche finito, essendo costituito, alla sua base, da unità minime di spaziotempo che interagiscono in maniera assolutamente locale, in modo non dissimile dalle celle di un AC.
L’idea non è in contrasto con le più recenti acquisizioni della fisica contemporanea – anzi, è una concezione della realtà cara a fisici del calibro di Albert Einstein ed Erwin Schroedinger. Anche recenti teorie della gravità quantistica ci dicono che tempo e spazio dovrebbero consistere appunto di quanti discreti. Se l’universo è fatto di celle come quelle di un AC, quanto saranno piccole? Se gli elettroni sono dell’ordine di grandezza (o magari di “piccolezza”) dei 10-15 metri, potremmo dover arrivare a 10-35 metri per le unità spaziali minime, e magari ai 10-44 secondi per le unità minime di tempo, coerentemente con la struttura teorica di Max Planck. In questa prospettiva la tanto cercata Teoria del Tutto - la teoria che unifica il comportamento di qualsiasi corpo fisico nella realtà che conosciamo - sarebbe dunque ottenuta "semplicemente" specificando le caratteristiche dell'automa cellulare che modella perfettamente il nostro universo.
E se l’universo è un AC, allora qualsiasi cosa esista è alla fin fine un aggregato più o meno grande di celle, le quali si evolvono sulla base di un ristretto numero di regole semplici e deterministiche. Esattamente come accade in Life, tutta la complessità del mondo deve discendere da una semplice sequenza di quattro elementi: spazio, tempo, stati e regole. Solo che ora stiamo parlando di alianti e rospi (e ghiande e navicelle spaziali e sedie e galassie e persone) assolutamente veri.
Se lo spazio è totalmente occupato da celle, sarebbe ragionevole ipotizzare che sia suddiviso in forme regolari, come avviene nei normali AC. Dato uno spazio a tre dimensioni, le forme regolari che possono suddividerlo senza lasciare “buchi” sono il tetraedro, il cubo e il dodecaedro rombico. A queste figure corrispondono, in due dimensioni, il triangolo equilatero, il quadrato, e l’esagono.
Nel nostro laboratorio, dopo vari esperimenti e simulazioni, abbiamo scelto il dodecaedro rombico e il suo corrispettivo bidimensionale, l’esagono. Queste figure hanno molti vantaggi nella rappresentazione del movimento, in particolare perché la distanza fra celle approssima il raggio di un cerchio. Prendiamo il caso a esagoni in due dimensioni: intorno a una cella ne esistono sei, equidistanti; a distanza di due unità spaziali ne esistono altre sei con lo stesso angolo e la stessa distanza fra loro, e così via. Che la realtà dello spazio sia così strutturata implica che, anche se il cerchio perfetto e la sfera perfetta non sussistono “nella realtà”, possono essere approssimati facilmente (vedi anche la sezione Esplora ).
Anche il tempo dovrà essere composto da unità minime, gli istanti. Come abbiamo visto parlando del gioco della vita di Conway, ha senso ritenere che la continuità nel movimento e nel cambiamento sia l’effetto “visibile”, a livello dimensionale superiore, di una serie di cambiamenti e movimenti discreti nelle celle o unità di base di un AC. Queste serie di cambiamenti potrebbero essere, da ultimo, sequenze di “salti” istantanei discreti e velocissimi.
In generale, la concezione per cui spazio e tempo sono composti di unità discrete è compatibile con l’idea che esista una massima velocità teorica raggiungibile, che stando alla teoria della relatività di Einstein sarebbe quella della luce.
In un universo come quello che stiamo descrivendo, il movimento è sempre apparente. Quello che possiamo etichettare come “spostamento” e che percepiamo nella realtà che ci circonda è, in realtà, cambiamento di stato da parte delle celle attraverso il tempo.
Stabilire quali sono gli stati e le regole delle celle che costituiscono l’universo è procedere per congetture. Naturalmente, al momento nessuno è in grado di andare a vedere che cosa fanno le celle minime del mondo! D’altra parte, tutta la ricchezza dell’universo osservabile dovrebbe essere riducibile, in un modo o nell’altro, agli stati e alle regole di base.
Se vale il motto simplex sigillum veri, il numero degli stati assumibili dalle celle dovrebbe essere finito, ma anche molto piccolo, e lo stesso dovrebbe valere per le regole. Se poi l’universo massimizza la propria efficienza computazionale, lo stato di ogni singola cella dovrebbe dipendere (dalle regole e) dallo stato delle celle immediatamente confinanti; nel caso bidimensionale, questo vuol dire: le sei celle che circondano ogni esagono.
Così diceva l’antico filosofo Parmenide nel Poema sulla natura, duemilacinquecento anni fa, e... iLabs concorda! L’idea di universo su cui scommette iLabs è centrata su un forte isomorfismo (ossia, su una “identità di struttura”) fra software (pensiero, informazione, mente) e hardware (realtà, fisica, corpo).
Se l’universo è un AC come quello che stiamo descrivendo, parlare di “proprietà fisiche degli oggetti”, e parlare di “distribuzione di informazione”, è parlare in due modi della stessa cosa. Da una parte, possiamo descrivere il mondo in termini di stati (degli atomi), dall’altra possiamo descriverlo in termini di contenuti di informazione implementati da (gruppi di) atomi, e di regole che operano su questi contenuti: ogni cambiamento nello stato fisico della materia corrisponde a un cambiamento nel contenuto di informazione, e viceversa.
Che questa intercambiambiabilità fra informazione e realtà accada è noto. Una istruzione software, ad esempio, può modificare lo stato della memoria di un computer (dunque, produrre modifiche sul piano fisico), che invierà, ad esempio, un segnale a una stampante; viceversa, una modifica della memoria di un computer può determinare la modifica del codice di un programma.
E le cose non vanno in modo molto diverso nel nostro corpo. Un pensiero può modificare lo stato fisico del nostro cervello, e questo può determinare una risposta razionale o emotiva realizzata nel nostro corpo – dal rossore involontario di un volto, a una sequenza organizzata e complessa di azioni come attraversare un incrocio, dipingere un quadro, o dimostrare un teorema. Viceversa, una modifica fisica del nostro cervello cambia i nostri pensieri; una modifica nel “software” genetico del DNA cambia l’organismo che risulterà dal corrispettivo sviluppo fisico.
| V. Per saperne di più | torna all'indice |
|---|
Per approfondire la Matematica dei Modelli di Riferimento e la cornice teorica in cui si inserisce i testi di riferimento sono ovviamente:
Berto F., Rossi G., Tagliabue J., La Matematica dei Modelli di Riferimento, Lampi di Stampa, 2010 >>
Canonico A., Rossi G., Semi-Immortalità. Il prolungamento indefinito della vita umana, Lampi di Stampa, 2007 >>
Presentiamo infine un elenco di testi e risorse su AC di vari livelli di difficoltà:
Giusto per cominciare
Game of Life di John Conway >> wiki - sito - codice NetLogo
La entry “Automi cellulari” su Wikipedia >>
La entry “Cellular Automaton” su MathWorld >>
Introduzioni più avanzate
Hopcroft J. E. e Ullman J. D., Introduction to Automata Theory, Languages, and Computation, Reading, MA: Addison Wesley, 1979 >>
Ilachinski A., Cellular Automata: A Discrete Universe, Singapore: World Scientific, 2001 >>
Preston, K. Jr. e Duff, M. J. B., Modern Cellular Automata: Theory and Applications, New York: Plenum, 1985 >>
Schiff. J.L., Cellular Automata: A Discrete View of the World, New York: Wiley Interscience, 2008 >>
Classici sugli AC
Crutchfield J.P. e Mitchell M., The Evolution of Emergent Computation, SFI Technical Report 94-03-012
Gardner M., The Game of Life, Parts I-III, Capp. 20-22 in Wheels, Life, and other Mathematical Amusements. New York: W. H. Freeman, 1983 >>
Toffoli T., e Margolus N., Cellular Automata Machines: A New Environment for Modeling, Cambridge, MA: MIT Press, 1987 >>
Von Neumann J., The Theory of Self-reproducing Automata, Urbana, IL: Univ. of Illinois Press, 1966 >>
Wolfram S., Cellular Automata and Complexity: Collected Papers, Reading, MA: Addison-Wesley, 1994 >>
Wolfram S., A New Kind of Science, Champaign, IL: Wolfram Media, 2002 >>
AC reversibili
Bennett C.H., Logical Reversibility of Computation, IBM Jour. Res. Dev. 6, 525-32, 1973
Bennett C.H., Thermodinamically Reversible Computation, Phy. Rev. Lett. 53, 1202, 1984
Fredkin E. e Toffoli T., Conservative Logic, Int. Jour. of Theo. Phy. 21, 219, 1982
Margolus N., Physics-Like Models of Computation, Physica 10D, 81-95, 1984
Margolus N., Physics and Computation, PhD thesis, Tech. Rep. MIT Lab. For Comp. Sci., March 1988
Toffoli T., Computation and Construction Universality of Reversible Cellular Automata, Jour. Comp. Sys. Sci. 15, 213, 1977
Toffoli T. e Margolus N., Invertible Cellular Automata, Physica D45, 229-53, 1990
| APPLET 2D | torna al top |
|---|
I. Specifiche dell'AC
I.I. Celle e intorno
I.II. Super-regola
I.III. Rappresentare gli operatori booleani
II. Implementazione
II.I. Il framework
II.II. Dettagli
II.III. Scarica la versione offline
II.IIII. Risoluzione problemi
III. Prova a...
III.I. Reversibilità forte
III.II. Formazione di pattern
| I. Specifiche dell'AC | torna all'indice |
|---|
I.I. Celle e intorno
La topologia del nostro universo, nella sua rappresentazione 2D, è a base esagonale (si veda anche l'introduzione della sezione Esplora). Questo differenzia il nostro automa da molti presenti in letteratura in almeno due punti essenziali: da una parte, la definizione di neighbourhood riflette perfettamente la topologia, per cui lo stato di una cella è determinato completamente dallo stato delle sei celle confinanti; dall'altra, la geometria - o, se si preferisce, fisica - dell'informazione si sviluppa secondi angoli e simmetrie molto diverse (rendendo più agevole, ad esempio, la creazione di moti circolari).
Per quanto riguarda la struttura logica della cella, il suo funzionamento è caratterizzato ad ogni istante di tempo dalla sequenza < percezione - pensiero - azione > - ovvero dal Modello di Riferimento più elementare. In particolare, la cella prima percepisce lungo i suoi lati i bit che arrivano da esagoni confinanti; quindi, la cella pensa quale azione intraprendere ed infine agisce, mappando in modo appropriato i bit in entrata su quelli in uscita. Ad ogni aggiornamento dell'automa dunque la cella utilizza 6 bit per memorizzare ciò che avviene nelle celle circostanti e 6 bit per esporre ai vicini il risultato del suo "pensiero": poichè l'universo non perde mai (se non quando, in una data implementazione, si raggiungono i confini di memoria) informazione il numero di bit della percezione è uguale al numero di bit coinvolti nell'azione - condizione necessaria, ma non sufficiente, perchè l'intero automa sia fortemente reversibile.
La regola che definisce l'evoluzione del sistema, da noi chiamata "super-regola", è dunque la seguente:
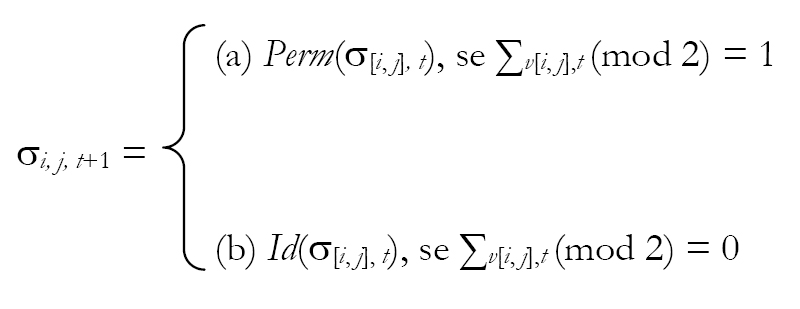
ovvero la somma modulo 2 dei valori (1 o 0) di chiascun membro della sestupla dei bit in entrata (ovvero i bit che costituiscono la percezione della cella). Id è un operatore che possiamo definire di identità, ovvero un operatore che rimanda ciascun sestupla in se stessa:
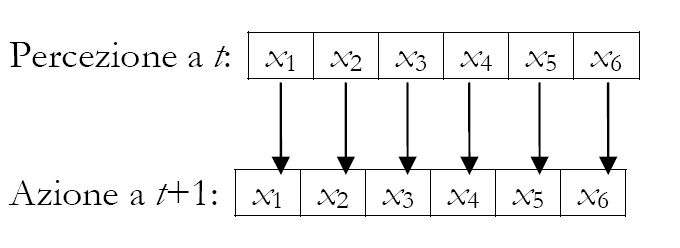
Perm invece è un operatore che possiamo definire di permutazione, ovvero un operatore che permuta gli elementi di ciascuna sestupla scambiando i primi tre con gli ultimi tre e viceversa:
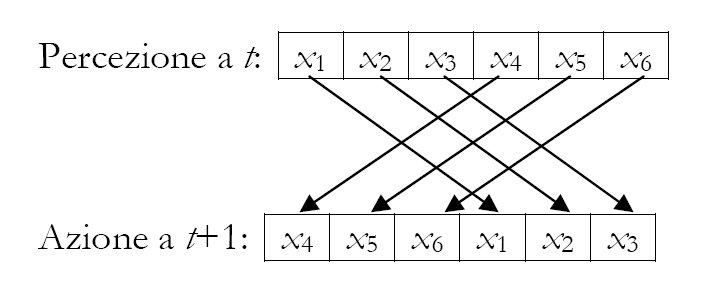
La super-regola permette la rappresentazione degli operatori booleani (e quindi permette all'automa cellulare di essere Turing-universale, ovvero in grado di computare qualsiasi funzione computabile) e rende l'universo perfettamente reversibile - cosa che si può sperimentare direttamente con l'applet invertendo il flusso del tempo e facendo ripartire l'automa, il quale darà l'impressione di "scorrere all'indietro" fino alle condizioni di partenza. Cosa vuol dire esattamente che la nostra super-regola è (fortemente) reversibile? Di norma, le regole che governano la dinamica degli AC sono irreversibili. La irreversibilità delle regole per AC è del tutto analoga a quella per un qualsiasi algoritmo o una qualsiasi funzione: una regola è detta irreversibile quando diversi input possono dar luogo allo stesso output. Quando ciò accade – e accade nella grande maggioranza dei casi: la regola di Life di Conway, ad esempio, non è reversibile; ma anche le più semplici funzioni booleane che troviamo anche nei motori di ricerca su internet, come AND e OR, non lo sono – non è in generale possibile, guardando solo alla configurazione di un automa al tempo t+1, stabilire quale fosse la sua configurazione a t. Un AND ci dà uno 0 in output. Qual era l’input? 0 e 1, 0 1 e 0, o due zeri? Tipicamente, le regole irreversibili non solo cancellano e scrivono bit di informazione nelle celle, ma lo fanno, appunto, in modo che non è in generale possibile recuperare l’informazione che è andata perduta. Abbiamo, insomma, una certo grado di “entropia informazionale”.
La nostra super-regola, al contrario, è non solo reversibile, ossia tale che a distinti input corrispondono sempre distinti output, ma anche fortemente tale. Una regola si dice fortemente reversibile (o time-reversal invariant, in inglese) quando è l’inversa di se stessa, ossia quando possiamo ottenere gli input di partenza a partire dagli output, applicando la stessa regola.
È chiaro in che senso questa proprietà è più forte della precedente. Quando una regola è fortemente reversibile, la sequenza di stati passati dell’AC può essere recuperata semplicemente invertendo il tempo, e lasciando che l’AC computi i propri stati secondo la propria regola. La stessa configurazione iniziale dell’universo può essere recuperata mediante un’evoluzione al contrario basata sulla stessa regola che lo governava quando il tempo scorreva “in avanti”: come se si facessero scorrere al contrario i fotogrammi di un film.
Naturalmente, configurazioni o sequenze o strutture periodiche di bit “attivi” e “inattivi” possono facilmente rappresentare segnali e quindi frammenti di informazione di ogni tipo, in quanto li realizzano fisicamente come stati e combinazioni di stati delle celle. Ora, ogni singola cella del nostro universo può essere vista come un gate logico – anzi, precisamente come un gate logico universale – proprio in quanto è un luogo di transizione (trasmissione o collisione) di bit e sequenze di bit di informazione che implementa la super-regola.
Cosa vuol dire che un gate logico è universale, per cominciare? Vuol dire che è in grado di rappresentare, come dicono i logici, un insieme “funzionalmente completo” di operatori booleani, ossia di calcolare tutte le funzioni booleane. È noto che insiemi come {AND, NOT} (congiunzione e negazione) o {OR, NOT} (disgiunzione e negazione) sono funzionalmente completi in questo senso.
Ora, trattiamo la singola cella qualsiasi del nostro AC come un gate che prende input da tre dei suoi sei lati, generando un output da altri tre. Supponiamo ad esempio che la cella individuata come prenda come input i segnali in arrivo dalle direzioni x, y e z qui segnate in grigio scuro, e restituisca come output i segnali che escono dai tre lati opposti, segnati in grigio chiaro:
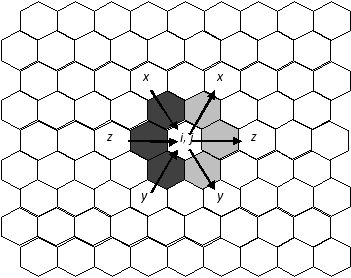
Siccome operatori come la negazione, NOT, hanno solo un input e un output, mentre operatori come la congiunzione, AND, hanno due input e un output, questo vuol dire intuitivamente che, quando vorremo simulare NOT o AND mediante la nostra super-regola implementata nelle celle, alcuni input e output saranno “pleonastici”. È facile mostrare che i primitivi della computazione, quali NOT, AND, ma anche il FAN-OUT di segnali, ossia il loro sdoppiamento (oltre a ritardi di segnale, deviazioni e rimbalzi di ogni tipo) possono essere realizzati nel nostro AC.
Prendiamo per esempio la congiunzione e la negazione, illustrate dai video sottostanti . Ogni cella del nostro universo può implementare una congiunzione logica, ossia un AND, reversibile: basta considerare l’input z come una “linea di controllo”, che viene attivata fissandone il valore in z = 1 (ossia facendo sopraggiungere in direzione z una sequenza di bit “attivi” o 1). In questo modo, considerando i bit in arrivo nelle direzioni x e y, la cella produce sia nella direzione di uscita x che nella direzione di uscita y un output che è la congiunzione di x e y: l’output di x (e di y) = 1 se e solo se l’input di x = 1 e quello di y = 1, altrimenti l’output di x (e di y) = 0. La negazione NOT può essere rappresentata secondo la stessa strategia: basta fissare z = 1 e y = 0. In questo modo l’output di z è la negazione dell’input di x, ossia se input x = 1, output z = 0, e se input x = 0, output z = 1.
| AND | NOT |
|---|
| II. Implementazione | torna all'indice |
|---|
II.I. Il framework
L'automa 2D è stato sviluppato attraverso la piattaforma NetLogo, un software completamente gratuito, creato da Uri Wilensky e mantenuto dall'Università di Northwestern. NetLogo mette a disposizione un linguaggio di modellazione esplicitamente pensato per i cosiddetti agent-based models, ovvero quei modelli scientifici in cui gli attori principali sono le componenti base del sistema in esame e gli effetti macroscopici emergono dalle interazioni che si svolgono al livello micro. Le possibilità offerte dall'ambiente di sviluppo sono pressochè senza fine; inoltre, grazie alla struttura particolarmente intuitiva dell'interfaccia e all'ottima documentazione online, NetLogo si è imposto come standard di fatto nell'insegnamento della modellazione scientifica nella università di tutto il mondo. In questo caso, NetLogo è stato preferito a soluzioni alternative perchè è molto usato - e quindi facilita la condivisione del codice ed il suo utilizzo in nuove applicazioni -, è "trasparente" - ovvero permette un codice che riproduca fedelmente la base teorica dell'AC in questione (ad es., il parallelismo) -, è basato su Java - quindi è facilmente importabile all'interno di un browser. Sfortunatamente, NetLogo è solo parzialmente compilato, e questo ne pregiudica notevolmente le prestazioni.
Lo stile di programmazione è stato scelto per mantenere la maggior trasparenza concettuale possibile del codice: chi avesse letto il libro o un articolo dettagliato sul funzionamento del nostro automa dovrebbe poter scorrere il codice in pochi minuti ed identificarne le funzioni chiave senza problemi. In particolare, al di là di tutte le funzioni "accessorie" (setup della griglia, importare/esportare configurazioni, filmati, verificare l'eventuale perdita di informazione, ecc.), il cuore del programma è costituito dalla funzione [go], la quale è a sua volta basata sulla funzione [super-regola].
[super-regola] ha due blocchi di codice, tra loro quasi-simmetrici: lo sdoppiamento è necessario per implementare la possibilità di far scorrere il tempo a ritroso in qualsiasi momento. In ciascun blocco vengono chiaramente identificati i momenti di < percezione - pensiero - azione > che caratterizzano le fondamenta concettuali della MMDR: durante la percezione ogni cella conta il numero dei bit in entrata; durante la fase successiva la cella decide sulla base della super-regola (il pensiero) quali bit esporre (l'azione). Sebbene soluzioni alternative garantiscano prestazioni migliori, l'attuale codice è probabilmente il miglior compromesso tra utilità pratica e fedeltà teorica.
La versione offline del nostro automa cellulare consente di salvare (e caricare da un file salvato) lo stato dell'universo in qualsiasi momento, facilitando così lo scambio di simulazioni interessanti nella comunità virtuale; in più è fornita la possibilità di esportare in formato .mov il video dell'evoluzione dell'universo. Il codice (in formato .nlogo) è open source l'ultima versione può essere scaricata qui. Commenti e segnalazioni possono essere inviati al nostro indirizzo mail dedicato.
II.IIII. Risoluzione problemi
Per poter visualizzare l'applet all'interno di un browser - Mozilla Firefox o Microsoft Explorer - è necessario aver installato il cosiddetto Java Runtime Environment (Java 6 o superiore): Java è una tecnologia gratuita inventata da Sun che permette la visualizzazione e il funzionamento di applicazioni interattive all'interno di normali finestre del proprio browser. La maggior parte degli utenti ha già installato questo diffusissimo componente: per verificarlo, basta andare sull'apposita pagina di test; nel caso in cui il test fallisca, è possibile scaricare ed installare il necessario in pochi minuti seguendo le indicazioni dello stesso sito. Oltre ad essere installato, Java deve anche essere abilitato dal vostro browser, ovvero non deve esserci nessun blocco di sicurezza che prevenga l'esecuzione di un'applicazione Java: per abilitare il JRE nel vostro browser seguite queste istruzioni. Se non voleste cambiare le vostre impostazioni, potete comunque utilizzare il nostro automa 2D scaricando la versione da utilizzare offline con NetLogo.
| III. Prova a... | torna all'indice |
|---|
III.I. Reversibilità forte
...generare esagoni utilizzando il setup random - l'effetto è particolarmente stupefacente con condizioni iniziali "complicate" - e fare evolvere l'universo per una decina di istanti. Quindi, inverti il flusso del tempo tramite reverse_time-flow e fai ripartire la simulazione per altrettanti istanti. Non importa quanti scontri, interazioni, pattern si siano formati: l'universo torna sempre perfettamente al suo "Big Bang".
...sperimentare tutte le configurazioni interessanti incluse nell'applet usando le diverse opzioni offerte dal menu di setup e poi a disegnare tu pattern interessanti dal punto di vista "fisico" e/o "computazionale" - usa l'opzione empty nel setup, poi clicca su draw! e dunque sulla/e cella/e che desideri inizializzare: a quel punto inserisci la sestupla di bit (ad es., "100111") che la cella espone ai vicini, clicca di nuovo su draw! e fai evolvere l'universo!. Potete segnalarci qui nuove configurazioni interessanti da includere nelle prossime release dell'AC - se si utilizza la versione offline, si possono esportare automaticamente con la comoda funziona inclusa.
| FAQ | torna al top |
|---|
I. Perchè l'AC iLabs ha base esagonale?
II. La super-regola mappa sestuple su sestuple: non è inusuale per un AC?
III. Perché è importante che l’AC sia reversibile?
IV. Cosa significa che l’AC è capace di computazione universale? Come lo sapete?
| I. Perchè l'AC iLabs ha base esagonale? | torna all'indice |
|---|
Se la natura è un AC e (come è plausibile assumere) gli atomi di base dividono uniformemente ed esaustivamente lo spazio, si tratterà di figure poligonali n-dimensionali; il che vuol dire che, al livello ultimo della realtà fisica, cerchi e curve, a rigore, “non esistono”. Fra le figure poligonali l’esagono (e il suo corrispettivo tridimensionale, il dodecaedro rombico) ha il vantaggio topologico di poter “simulare” curve e circonferenze al meglio, visto che ogni cella-esagono è circondata da sei compagne equidistanti dal suo centro. Anche gli angoli retti in questo universo, “non esistono” al livello base ma, naturalmente, possono essere facilmente approssimati a loro volta.
| II. La super-regola mappa sestuple su sestuple: non è inusuale per un AC? | torna all'indice |
|---|
Sì è inusuale; l’idea portante è che la operazione propria di ogni cella (il suo pensiero) sia mappare una struttura (le proprie percezioni) su un’altra struttura isomorfa alla prima (le azioni).Proprio questa originale definizione del neighbourhood per una cella consente di ottenere la reversibilità forte della regola che anima l’universo: non vi è alcuna perdita di struttura (e quindi, di informazione) quando la regola viene applicata.
| III. Perché è importante che l’AC sia reversibile? | torna all'indice |
|---|
Per due ragioni: la prima è che la computazione non reversibile è un dispendio di energia. A qualsiasi livello fisico, quando un bit di viene cancellato si genera un certo minimo quantitativo di “entropia informazionale”, e l’informazione perduta viene dispersa nell’ambiente sotto forma di calore. La computazione reversibile minimizza il dispendio energetico ed è quindi più efficiente in lunea di principio.
La seconda ragione è che le leggi della meccanica sono reversibili a livello microfisico (sia nell’interpretazione classica, che in quella quantistica), il che vuol dire che una computazione fisicamente realizzata in modo irreversibile (distinti stati iniziali che danno un medesimo stato finale) non può adeguare ciò che accade ai livelli minimi della realtà fisica. Viceversa, se l’attività reale dell’universo è computazione fin dai suoi livelli dimensionali ultimi, un modello che rappresenti quest’attività dovrà essere basato su computazioni reversibili.
| IV. Cosa significa che l’AC è capace di computazione universale? Come lo sapete? | torna all'indice |
|---|
Beh, lo abbiamo mostrato costruttivamente, in modo analogo a come è stato fatto, a suo tempo, per mostrare che Life di Conway è capace di computazione universale. La strategia consiste nel mostrare che pattern di stati di celle nell’AC sono in grado di simulare i componenti di base della computazione standard in un framework non standard come quello cellulare, caratterizzato da un massiccio parallelismo: trasferimento di segnali in (nella simulazione di) circuiti, configurazioni stabili o periodiche di stati per la memoria, e la possibilità di processare i segnali attraverso (la realizzazione di) un insieme funzionalmente completo di gate logici. Avere computazione universale è importante perché implica che l’AC rilevante può valutare tutte le funzioni computabili, e quindi realizzare una macchina di Turing universale.

