Esplora
|
|---|
INDICE
PREFAZIONE
0. INTRODUZIONE
0.1. L’universo fisico
0.1.1. Computation everywhere
0.1.2. Un universo discreto
0.1.3. Spazio e tempo
0.1.4. Stati e regole
0.2. Il nostro primo approccio ai MdR
1. COMPUTAZIONE UNIVERSALE
1.1. La teoria degli automi cellulari: per una “fisica del pensiero”
1.2. Universo digitale
1.3. La notazione funzionale per i MdR
1.4. Le quattro caratteristiche dell’universo
1.5. Reversibilità, debole e forte, dei MdR
1.6. Super-regola: il MdR fondamentale
1.7. Proprietà della super-regola
1.8. Reversibilità e fisica dell’informazione
1.9. Computazione universale
1.9.1. Congiunzione
1.9.2. Negazione
1.9.3. Fan-out
1.9.4. Delays
1.10. Conclusioni
2. IL FORMALISMO COMPUTAZIONALE
2.1. Sintassi
2.2. Alfabeto
2.3. Regole di formazione
2.3.1. Termini individuali
2.3.2. Formule
2.3.3. Specifiche sulla sintassi
2.4. Computabilità della sintassi
2.5. La struttura assiomatica e definitoria
2.6. Le regole d’inferenza
3. L'ONTOLOGIA DEI MODELLI DI RIFERIMENTO
3.1. Assiomi lessicali
3.2. Atomi-celle
3.3. Iper-estensionalità
3.4. Individuabilità, sequenzialità, istantaneità
3.5. Convenzionalismo
3.5.1. Composizione mereologica non ristretta
3.5.2. Cookie-cutting arbitrario
3.6. Sistema, interno, esterno
4. MODELLI DI RIFERIMENTO RICORSIVI
4.1. Modelli di riferimento equivalenti
4.1.1. Equivalenze convenzionali fra MdR
4.1.2. Stimare la complessità dei MdR
4.2. Modelli di riferimento parziali e inversi
4.3. Modelli ricorsivi
4.3.1. Percezioni, azioni, e numeri
4.3.2. Ricorsività di base e universo cellulare
4.3.3. Definizioni successive di MdR ricorsivi
4.3.4. Caratterizzazione dei MdR logici via ricorsione
4.4. La rappresentabilità formale dei MdR ricorsivi
4.5. Metamodelli di riferimento
4.5.1. La codifica dei MdR
4.6. MdR parziali e ricorsività
4.7. Univ: il MdR ricorsivo universale
4.8. Punto fisso: l’autoreferenza ricorsiva
5. GENERALIZZAZIONI: PILLOLE DI ALGEBRA DEI MDR
5.1. Caratterizzazioni algebriche di sottoteorie dei MdR
5.2. I MdR come omomorfismi e isomorfismi: alla radice dell’intelligenza?
5.3. Passaggio
APPENDICE I. PRIMI PASSI VERSO L'I-ESE
I.1. Cognizione e informazione
I.2. Semantica
I.2.1. Modello formale
I.2.2. Semantica tarskiana via ricorsione
I.2.2.1. Significato dei termini individuali
I.2.2.2. Significato delle formule, verità, validità, conseguenza logica
I.2.3. Specifiche sulla semantica
I.2.4. Computabilità della semantica
I.3. MdR primitivi, MdR derivati
APPENDICE II: IL GRAFENE
APPENDICE III. BIOLOGIA
III.1 Computazione nelle cellule: wetware
III.2 MdR negli organismi unicellulari
III.3 Percezione cellulare
III.4 Transistor proteici
III.5 Copia, complessità, ricorsività: alla ricerca del MdR vita
III.6 Vita, biologia e nanotecnologia
APPENDICE IV: LA MMDR ONLINE
RIFERIMENTI
| PREFAZIONE | torna all'indice |
|---|
Il libro che avete tra le mani non nasce per caso. Non abbiamo sviluppato la matematica dei modelli di riferimento canticchiando sotto la doccia o grazie ad incontri fortuiti, magari avvenuti in campi scientifici collaterali. Sarebbero state storielle divertenti da raccontare nella prefazione. E invece no. Indipendentemente dalla qualità del risultato raggiunto, la matematica dei modelli di riferimento è stata sviluppata giorno dopo giorno, mattoncino dopo mattoncino. La storia di questo libro è “solo” una storia di continui passaggi successivi, di ripetute stratificazioni; forse d’ingegno, sicuramente di volontà e determinazione a raggiungere il risultato.
Abbiamo sviluppato la matematica dei modelli di riferimento semplicemente perché ne avevamo bisogno. Nessun premio famoso da vincere, nessuna cattedra da conquistare, men che meno finanziamenti da attirare. Ci serviva e basta: puro strumento funzionale. Devo piantare un chiodo? Mi serve un martello. Devo conservare a lungo i cibi? Mi serve un frigorifero. Devo riprodurre completamente la mente umana? Mi serve una matematica in grado di farlo; una matematica che racchiuda in sé, ampliandola, qualsiasi altro tipo di matematica precedentemente sviluppata.
Un obiettivo troppo ambizioso? Forse sì, ma dopo che si è assunto come possibile – improbabile, ma possibile – il prolungamento indefinito della vita umana, nessuna sfida cognitiva può spaventare a priori.
Non sono neppure un caso le possibili ricadute applicative della nostra matematica. Come abbiamo cercato di mostrare nel libro, deve poter descrivere quello che fino ad oggi siamo in grado abitualmente di descrivere con le “altre matematiche”. Inoltre, come ci aspettiamo dagli sviluppi futuri, deve essere in grado di rappresentare “nativamente” un possibile modello di universo fisico, non in contraddizione con le nostre attuali conoscenze sperimentali, ed essere in grado di descrivere qualsiasi tipo di attività cognitiva che la nostra mente svolge, comprese quelle appartenenti alle sfere più intime della creatività, dell’intuito e delle emozioni.
Questa impostazione potrebbe suonare strana ai lettori che non si occupano di computazione. Però se assumiamo, anche solo per pochi istanti, la possibilità che “a livello più basso tutto funzioni allo stesso modo” la nostra impostazione dovrebbe apparire meno bizzarra. La matematica è una delle scienze più affascinanti e artistiche elaborate dagli uomini. Molti la definiscono “la scienza” per eccellenza. Dal nostro punto di vista la matematica è soprattutto uno strumento indispensabile per capire il funzionamento dell’universo e per capire il funzionamento della nosta mente che cerca di indagarlo. E magari per riuscire a vincere il “premio” della Semi-Immortalità.
Abbiamo sviluppato la matematica dei modelli di riferimento semplicemente perché ne avevamo bisogno. Nessun premio famoso da vincere, nessuna cattedra da conquistare, men che meno finanziamenti da attirare. Ci serviva e basta: puro strumento funzionale. Devo piantare un chiodo? Mi serve un martello. Devo conservare a lungo i cibi? Mi serve un frigorifero. Devo riprodurre completamente la mente umana? Mi serve una matematica in grado di farlo; una matematica che racchiuda in sé, ampliandola, qualsiasi altro tipo di matematica precedentemente sviluppata.
Un obiettivo troppo ambizioso? Forse sì, ma dopo che si è assunto come possibile – improbabile, ma possibile – il prolungamento indefinito della vita umana, nessuna sfida cognitiva può spaventare a priori.
Non sono neppure un caso le possibili ricadute applicative della nostra matematica. Come abbiamo cercato di mostrare nel libro, deve poter descrivere quello che fino ad oggi siamo in grado abitualmente di descrivere con le “altre matematiche”. Inoltre, come ci aspettiamo dagli sviluppi futuri, deve essere in grado di rappresentare “nativamente” un possibile modello di universo fisico, non in contraddizione con le nostre attuali conoscenze sperimentali, ed essere in grado di descrivere qualsiasi tipo di attività cognitiva che la nostra mente svolge, comprese quelle appartenenti alle sfere più intime della creatività, dell’intuito e delle emozioni.
Questa impostazione potrebbe suonare strana ai lettori che non si occupano di computazione. Però se assumiamo, anche solo per pochi istanti, la possibilità che “a livello più basso tutto funzioni allo stesso modo” la nostra impostazione dovrebbe apparire meno bizzarra. La matematica è una delle scienze più affascinanti e artistiche elaborate dagli uomini. Molti la definiscono “la scienza” per eccellenza. Dal nostro punto di vista la matematica è soprattutto uno strumento indispensabile per capire il funzionamento dell’universo e per capire il funzionamento della nosta mente che cerca di indagarlo. E magari per riuscire a vincere il “premio” della Semi-Immortalità.
| UN UNIVERSO DISCRETO | torna all'indice |
|---|
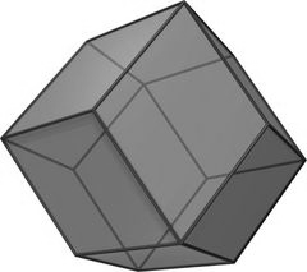 Come concepire un universo in cui materia e informazione sono due facce della stessa medaglia? Ecco la proposta iLabs. L’universo (diciamo, U) dev’essere, per cominciare, discreto e finito – basato su unità minime di spaziotempo (quanto “minime”? 10-35 m per l’unità spaziale minima, e 10-44 secondi per quella temporale minima, potrebbero essere buone ipotesi di partenza; ma quali siano di preciso queste dimensioni ha un’importanza teorica limitata).
Come concepire un universo in cui materia e informazione sono due facce della stessa medaglia? Ecco la proposta iLabs. L’universo (diciamo, U) dev’essere, per cominciare, discreto e finito – basato su unità minime di spaziotempo (quanto “minime”? 10-35 m per l’unità spaziale minima, e 10-44 secondi per quella temporale minima, potrebbero essere buone ipotesi di partenza; ma quali siano di preciso queste dimensioni ha un’importanza teorica limitata).Chiamiamo celle questi atomi. Ci aspettiamo che lo spazio sia interamente occupato da celle morfologicamente identiche. Esiste dunque un numero finito w di celle, ossia di unità spaziotemporali minime. Dunque, anche il tempo è diviso in unità discrete minimali, gli istanti: t0, t1, ... (algebricamente: il tempo è un ordine lineare discreto). Il nostro spazio euclideo intuitivo è tridimensionale. Ma un universo discreto può anche avere la forma di uno spazio a una, due, tre, … n dimensioni dal punto di vista computazionale. Per modellare il nostro universo, abbiamo scelto una griglia esagonale bidimensionale, ma i risultati ottenuti dalla nostra ricerca sarebbero realizzabili anche implementando i nostri MdR in griglie quadratiche tradizionali, e anche in un ambiente a tre dimensioni suddiviso dall’analogo tridimensionale dell’esagono: il dodecaedro rombico. Esagono e dodecaedro rombico hanno svariati vantaggi topologici nella rappresentazione del movimento fisico – specificamente, la distanza fra celle può essere approssimata in termini di raggio:
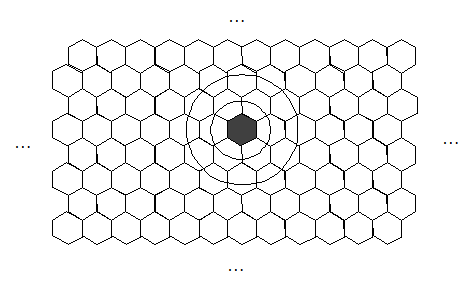
Una volta fissata una base dello spazio, in un contesto bidimensionale ogni cella è univocamente individuata come punto in un reticolo da una coppia ordinata di numeri interi < i, j >. Ad ogni istante di tempo t, ogni cella < i, j > si trova in uno e un solo stato σ ∈ Σ , dove Σ è un insieme finito di stati discreti di cardinalità k. Indicheremo con “σ i, j, t” lo stato della cella < i, j > al tempo t.
La nostra prospettiva è schiettamente convenzionalista: anzitutto, riteniamo che la sterminata varietà degli oggetti del mondo intorno a noi, con le loro proprietà, qualità e caratteristiche, emerga come una risultanza “di alto livello” di questi semplici ingredienti di base: celle atomiche, e un limitato numero di stati di base da esse istanziati. In secondo luogo, tutto è, da ultimo, un aggregato di celle. Chiamiamo sistema un qualsiasi aggregato. Allora, qualsiasi sistema è tanto “legittimo” quanto qualsiasi altro: i nostri oggetti ordinari sono semplicemente quegli aggregati che si accordano meglio col modo in cui suddividiamo il reale – e questo dipende dal nostro apparato cognitivo, dalle nostre capacità di apprendimento, e dai nostri interessi pratici.
L’universo non funziona a caso: regole precise determinano come ogni punto del reticolo aggiorna il proprio stato. Non sappiamo quali siano le regole di base, ma sappiamo per certo che devono essere modelli di riferimento: sequenze deterministiche di input, elaborazioni ed output. Ora, la nostra scommessa è che, al livello base della realtà, le regole debbano essere poche e semplici; complessità e varietà dovrebbero emergere a livelli superiori e dipendere dalla semplicità sottostante: simplex sigillum veri.
Non ci sono misteriose “azioni a distanza” nell’universo, ma solo interazioni locali: ogni punto < i, j > interagisce solo con le sei celle adiacenti, chiamate il suo neighbourhood:
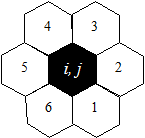
Indichiamo con “[i, j]” il neighbourhood del punto < i, j >. Allora, una regola deterministica dinamica o MdR governa gli atomi – e dunque, il mondo: ad ogni istante t, ogni punto < i, j > aggiorna in sincrono il proprio stato rispetto all’istante t-1, seguendo un’unica regola o MdR φ:Σ→Σ, tale che per ogni σ, < i, j >, e t:
σ i, j, t+1 = φ(σ [i, j], t)
Il nostro mondo ospita una quantità globalmente finita di informazione: data k la cardinalità di Σ e un numero w di punti del reticolo, abbiamo al massimo kw configurazioni globali per l’universo U. Di conseguenza, l’intera evoluzione di U è un grafo di transizione globale finito, GΦ - il grafico della funzione di transizione globale Φ:Γ→Γ(dove Γ è il phase space o l’insieme delle configurazioni globali di U) indotta dal MdR Φ.
| COMPUTAZIONE UNIVERSALE | torna all'indice |
|---|
Le leggi dinamiche della fisica sono reversibili a livello microscopico: distinti stati iniziali in un sistema microfisico portano sempre a distinti stati finali. È probabile che qualsiasi modello formale che miri a catturare le computazioni che hanno realmente luogo alle radici della realtà debba ospitare una dinamica reversibile. D’altra parte, la computazione irreversibile comporta sempre uno spiacevole dispendio energetico. Un AND ci dà 0 come output a t+1. Qual era l’input a t? 0 e 1, o viceversa, o due zeri? Come aveva già mostrato von Neumann, questa “entropia informazionale” costa ~3 • 10-21 joules per ogni passo computazionale elementare a temperatura ambiente.
La perdita di informazione ha un costo termodinamico da pagare in termini di energia, per così dire, “non computazionale”. La qual cosa non dipende da inefficacia nel design dei circuiti: segue direttamente dall’esistenza di computazioni irreversibili. Man mano che la tecnologia avanza, il problema dell’entropia informazionale è destinato a farsi vivo: potremmo aver bisogno di processori reversibili prima di quanto si creda.
Abbiamo sviluppato un modello matematico (un automa cellulare a stati finiti) dotato di una dinamica perfettamente reversibile e capace di conservare la totalità dell’informazione archiviata all’inizio dell’universo. Quindi, abbiamo fornito una dimostrazione effettiva del fatto che il nostro automa è capace di computazione universale: il nostro universo discreto computazionale può ospitare macchine di Turing universali, capaci di computare (data la Tesi di Turing) tutto ciò che è computabile. Ciò dipende dal fatto che ogni singola cella del nostro universo istanzia un singolo MdR come primitivo computazionale. Il nostro modello è quindi un buon candidato per la realizzazione di sistemi computazionali ad alte prestazioni: sistemi capaci di ospitare circuiti logici che computano con dissipazione di energia interna virtualmente nulla.
Abbiamo sviluppato un modello matematico (un automa cellulare a stati finiti) dotato di una dinamica perfettamente reversibile e capace di conservare la totalità dell’informazione archiviata all’inizio dell’universo. Quindi, abbiamo fornito una dimostrazione effettiva del fatto che il nostro automa è capace di computazione universale: il nostro universo discreto computazionale può ospitare macchine di Turing universali, capaci di computare (data la Tesi di Turing) tutto ciò che è computabile. Ciò dipende dal fatto che ogni singola cella del nostro universo istanzia un singolo MdR come primitivo computazionale. Il nostro modello è quindi un buon candidato per la realizzazione di sistemi computazionali ad alte prestazioni: sistemi capaci di ospitare circuiti logici che computano con dissipazione di energia interna virtualmente nulla.
| ONTOLOGIA FORMALE | torna all'indice |
|---|
Un modello di universo in cui realtà fisica e realtà informazionale sono strettamente collegate è un candidato ideale a rappresentare non solo funzioni ed algoritmi, ma anche concetti e proprietà - ovviamente tramite la loro formalizzazione e computazione! Accanto al formalismo tipico degli automi cellulari abbiamo dunque sviluppato una teoria formale - un'ontologia vera e propria - in cui rappresentare gli oggetti e le proprietà che costituiscono il nostro universo.
Il framework mereologico utilizzato nella modellizzazione è classico e intuitivo. Una mereologia è una teoria che caratterizza la nozione, quindi il MdR, parte, e può essere regolarmente assiomatizzata. Attraverso questo primitivo si procede dunque alla definizione formale di altre nozioni fondamentali – nozioni come quelle di atomo, sistema, interno ed esterno, prima caratterizzate solo intuitivamente.
Sfruttando la frattalità dei MdR crediamo che l'approccio si possa generalizzare fino a rappresentare un gran numero di oggetti, proprietà ed eventi: l'ontologia iLabs è il primo, indispensabile, passo verso una sistema di conoscenza perfettamente computabile.
Il framework mereologico utilizzato nella modellizzazione è classico e intuitivo. Una mereologia è una teoria che caratterizza la nozione, quindi il MdR, parte, e può essere regolarmente assiomatizzata. Attraverso questo primitivo si procede dunque alla definizione formale di altre nozioni fondamentali – nozioni come quelle di atomo, sistema, interno ed esterno, prima caratterizzate solo intuitivamente.
Sfruttando la frattalità dei MdR crediamo che l'approccio si possa generalizzare fino a rappresentare un gran numero di oggetti, proprietà ed eventi: l'ontologia iLabs è il primo, indispensabile, passo verso una sistema di conoscenza perfettamente computabile.
| MODELLI DI RIFERIMENTO RICORSIVI | torna all'indice |
|---|
Intuitivamente, un MdR ricorsivo è un MdR che “si riferisce a se stesso” nella propria definizione. Un po’ più precisamente: un MdR ricorsivo è un MdR tale che le sue azioni od output sulla base di certe percezioni od input possono essere determinate dall’output o azione di quello stesso MdR rispetto a input o percezioni più semplici: quello che un MdR ricorsivo fa per certe percezioni più complesse dipende da quello che esso stesso fa, o farebbe, per percezioni più semplici. I MdR ricorsivi possono essere introdotti, quindi, con definizioni ricorsive standard: l’operatore nel definiendum ricorre nel definiens.
Catturando integralmente la teoria degli operatori ricorsivi, la matematica dei MdR permette di definire la nozione fondamentale di meta-modello. Informalmente, un meta-modello non è altro che un modello di riferimento capace di percepire altri modelli di riferimento e di operare su di essi. Tecnicamente, ciò è stato ottenuto codificando i MdR stessi come stati delle celle che abitano il nostro universo digitale U: un meta-modello può quindi prendere come input i codici dei MdR che percepisce.
Incorporando il Teorema di Ricorsione (Forte) di Kleene nella teoria dei MdR, è stato quindi dimostrato che ci può essere un MdR universale, capace di emulare i pensieri di qualsiasi MdR ricorsivo. Questo è un MdR (parziale) della seguente forma:
univ(e, < x1, ..., xn>).
Dato un MdR ricorsivo n-ario f(x1, ..., xn) con codice e, ossia, [e]n(x1, ..., xn), univ prende come input il codice di f e (il codice per) il suo input, e fornisce come output quello che sarebbe dato da f o [e]n:
f(x1, ..., xn) ≅ [e]n(x1, ..., xn) ≅ univ(e, < x1, ..., xn>).
Ovviamente, univ corrisponde a una MTU e, dati i risultati di computabilità universali ottenuti per U, può dunque essere realizzato nel nostro universo digitale.
Catturando integralmente la teoria degli operatori ricorsivi, la matematica dei MdR permette di definire la nozione fondamentale di meta-modello. Informalmente, un meta-modello non è altro che un modello di riferimento capace di percepire altri modelli di riferimento e di operare su di essi. Tecnicamente, ciò è stato ottenuto codificando i MdR stessi come stati delle celle che abitano il nostro universo digitale U: un meta-modello può quindi prendere come input i codici dei MdR che percepisce.
Incorporando il Teorema di Ricorsione (Forte) di Kleene nella teoria dei MdR, è stato quindi dimostrato che ci può essere un MdR universale, capace di emulare i pensieri di qualsiasi MdR ricorsivo. Questo è un MdR (parziale) della seguente forma:
univ(e, < x1, ..., xn>).
Dato un MdR ricorsivo n-ario f(x1, ..., xn) con codice e, ossia, [e]n(x1, ..., xn), univ prende come input il codice di f e (il codice per) il suo input, e fornisce come output quello che sarebbe dato da f o [e]n:
f(x1, ..., xn) ≅ [e]n(x1, ..., xn) ≅ univ(e, < x1, ..., xn>).
Ovviamente, univ corrisponde a una MTU e, dati i risultati di computabilità universali ottenuti per U, può dunque essere realizzato nel nostro universo digitale.
| AUTOREFERENZA RICORSIVA E OLTRE | torna all'indice |
|---|
L’autoreferenza ricorsiva è la situazione che ha luogo quando un MdR non soltanto richiama se stesso, ma è “consapevole” di farlo – cosicché un sistema che lo implementa si può “accorgere” di ciò che sta facendo mediante quello stesso MdR.
Daccapo, questo non è animismo semantico. Infatti, espressioni come “è consapevole” possono ottenere un significato matematico ben preciso. Molta della ricerca condotta da iLabs è guidata dalla persuasione che l’autoreferenza ricorsiva sia alla base di ciò che ordinariamente chiamiamo “coscienza”: una differenza essenziale fra l’attività coscienziale e un qualsiasi altra procedura computazionale consiste nel fatto che la nostra mente, in quanto (auto)cosciente, ha la capacità di pensare, di avere un punto di vista su, se stessa – probabilmente con limiti operativi alla capacità di operare sul proprio “codice sorgente”. Se l’Intelligenza Artificiale si deve realizzare, lo farà attraverso l’autoreferenza ricorsiva – o questa è la nostra scommessa.
I Teoremi di Ricorsione, applicati ai nostri MdR ricorsivi, garantiscono che possiamo definire MdR parziali che sono ricorsivamente autoreferenziali, perché includono il proprio stesso codice nelle proprie definizioni ricorsive. Queste sono, semplicemente, definizioni per punto fisso. Dato che i codici numerici sono percezioni prese in input da (meta-)modelli di riferimento, che possono anche emulare le procedure di pensiero effettuate dai MdR codificati, i MdR ricorsivamente autoreferenziali possono percepire se stessi in senso matematicamente preciso, e rappresentare in sé la stessa procedura computazionale in cui consistono.
Daccapo, questo non è animismo semantico. Infatti, espressioni come “è consapevole” possono ottenere un significato matematico ben preciso. Molta della ricerca condotta da iLabs è guidata dalla persuasione che l’autoreferenza ricorsiva sia alla base di ciò che ordinariamente chiamiamo “coscienza”: una differenza essenziale fra l’attività coscienziale e un qualsiasi altra procedura computazionale consiste nel fatto che la nostra mente, in quanto (auto)cosciente, ha la capacità di pensare, di avere un punto di vista su, se stessa – probabilmente con limiti operativi alla capacità di operare sul proprio “codice sorgente”. Se l’Intelligenza Artificiale si deve realizzare, lo farà attraverso l’autoreferenza ricorsiva – o questa è la nostra scommessa.
I Teoremi di Ricorsione, applicati ai nostri MdR ricorsivi, garantiscono che possiamo definire MdR parziali che sono ricorsivamente autoreferenziali, perché includono il proprio stesso codice nelle proprie definizioni ricorsive. Queste sono, semplicemente, definizioni per punto fisso. Dato che i codici numerici sono percezioni prese in input da (meta-)modelli di riferimento, che possono anche emulare le procedure di pensiero effettuate dai MdR codificati, i MdR ricorsivamente autoreferenziali possono percepire se stessi in senso matematicamente preciso, e rappresentare in sé la stessa procedura computazionale in cui consistono.