TABLE OF CONTENTS
FOREWORD
0. INTRODUCTION
0.1. The physical universe
0.1.1. Computation everywhere
0.1.2. A discrete universe
0.1.3. Space and time
0.1.4. States and rules
0.2. Our first approach to MoR
1. UNIVERSAL COMPUTATION
1.1. The theory of cellular automata: towards a “physics of thought”
1.2. Digital universe
1.3. Functional notation for the MoR
1.4. The four characteristics of the universe
1.5. Weak and strong reversibility of MoR
1.6. Super-rule: the fundamental MoR
1.7. Properties of the super-rule
1.8. Reversibility and the physics of information
1.9. Universal computation
1.9.1. Conjunction
1.9.2. Negation
1.9.3. Fan-out
1.9.4. Delays
1.10. Conclusions
2. COMPUTATIONAL FORMALISM
2.1. Syntax
2.2. Alphabet
2.3. Formation rules
2.3.1. Individual terms
2.3.2. Formulas
2.3.3. Details on the syntax
2.4. Computability of the syntax
2.5. The axiomatic and definitory structure
2.6. Inference rules
3. ONTOLOGY OF THE MODELS OF REFERENCE
3.1. Lexical axioms
3.2. Atom-cells
3.3. Hyper-extensionality
3.4. Individuability, sequentiality and istantaneity
3.5. Conventionalism
3.5.1. Unrestricted mereological composition
3.5.2. Arbitrary cookie-cutting
3.6. System, internal, external
4. RECURSIVE MODELS OF REFERENCE
4.1. Equivalent models of reference
4.1.1. Conventional equivalences between MoR
4.1.2. Estimating the complexity of MoR
4.2. Partial and inverse MoR
4.3. Recursive models
4.3.1. Perceptions, actions and numbers
4.3.2. Basic recursion and the cellular universe
4.3.3. Successive definitions of recursive MoR
4.3.4. Characterization of logical MoR via recursion
4.4. Formal representability of recursive MoR
4.5. Metamodels of reference
4.5.1. The encoding of MoR
4.6. Partial MoR and recursion
4.7. Univ: the universal recursive MoR
4.8. Fixed point: recursive self-reference
5. GENERALIZATIONS: BITS ALGEBRA OF MoR
5.1. Algebraic characterizations of sub-theories of the MoR
5.2. The MoR as homomorphims and isomorphisms: at the root of intelligence?
5.3. Passage
APPENDIX I. FIRST STEPS TOWARDS I-ESE
I.1. Cognition and information
I.2. Semantics
I.2.1. Formal model
I.2.2. Tarskian semantics via recursion
I.2.2.1. Meaning of individual terms
I.2.2.2. Meaning of formulas, truth, validity, logical consequence
I.2.3. Specifications on the semantics
I.2.4. Computability of the semantics
I.3. Primitive MoR, derived MoR
APPENDIX II: GRAPHENE
APPENDIX III. BIOLOGY
III.1 Computation in the cells: wetware
III.2 MoR in the unicellular organisms
III.3 Cellular perception
III.4 Protein transistors
III.5 Copy, complexity, recursion: in quest of the MoR life
III.6 Life, biology and nanotechnology
REFERENCES
| FOREWORD | back to top |
|---|
The mathematics of the models of reference has been formulated at iLabs Milan,
a private research lab in applied Artificial Intelligence devoted to the
achievement of the indefinite extendibility of human life-span. It has
been developed via a series of successive extensions, starting with an
imaginative insight. We have envisaged it mainly as a tool – with no
special prize to win, position to conquer, or possible fundraising in mind:
we just needed it as an instrument. One needs a fridge in order to preserve
one’s food; a hammer in order to hammer nails; and a mathematics
that can recapture previously developed mathematical techniques, in
order to completely reproduce the human mind. An ambitious task
indeed – but once the indefinite extendibility of life has been assumed as
possible, as we do in our lab, no cognitive endeavor can be frightening a
priori.
The possible applications of the mathematics of the models of reference are of major importance to us: as we begin to show in the book, it should not only recapture other kinds of mathematics, but also allow us to represent a possible model of the physical universe itself – a model that does not contradict our current, established experimental and scientific knowledge. It should also allow us to describe our mind’s cognitive activities, including those relating to such fields as creativity, intuition, and emotions.
We expect readers interested in computation in general to be puzzled by such a framework. However, if we provisionally assume that, at the bottom level of reality, “everything behaves alike”, our theoretical option might not look so bizarre. Mathematics is one of the most fascinating human enterprises, but from our viewpoint it is, first of all, the tool to understand the behavior of reality, as well as of our mind investigating reality – perhaps in order to win the prize of the endless extension of human life-span.
The Introduction of our book informally presents the theoretical pillars of our theory, to be developed in subsequent Chapters: the notion of Model of Reference (for which we will often use the abbreviation “MoR” for convenience, without distinction between singular and plural) which is – behind a somewhat unusual terminology – the general idea of a deterministic, algorithmic operator; and the discrete universe hypothesis, which we take from such classic – albeit non-standard – approaches to the physics of computation as Stephen Wolfram’s New Kind of Science, Konrad Zuse’s works, and the by now well-established theory of cellular automata.
In Chapter 1, we describe the cellular automaton developed in our lab. We explore some of its basic mathematical features, highlighting in particular the strong reversibility of its dynamic rule, i.e., the fact that not only distinct initial states in the evolution of the automaton lead to distinct final states, but also, any configuration of the automaton can be regained by running it backwards via the very same dynamic rule. Strong reversibility, as we explain there, is highly desirable both for theoretical and for practical reasons.
Next, we show how, by implementing such a rule, the automaton is capable of universal computation, i.e., it can simulate a universal Turing machine and compute (if Turing’s Thesis is right) anything computable, insofar as each cell of the automaton acts as a universal and reversible logical gate. The strategy we follow is the same as the one used by Berkelamp, Conway and Guy in their constructive proof that Conway’s celebrated cellular automaton, The Game of Life, is computation-universal: it consists in showing how all the basic building bricks of computation (memory, circuits, logical gates) can be emulated by patterns and configurations of (states of) the elementary cells of the automaton.
Chapter 2 introduces the formal symbolism used in the following: this is the canonical notation of first-order logic with identity and function symbols. The choice of the standard notation of elementary logic in a mathematical book is theoretically motivated: in the development of the book, the principles of our theory are introduced as non-logical, firstorder axioms that work as constraints on the admissible models, whereas the rules of first-order logic (the chosen form is classical natural deduction), being sound and complete, in principle allow one to infer all the axioms’ logical consequences.
Chapter 3 presents, in the form of a set of such axioms, the formal ontology underlying our automaton. This is a mereological framework describing a discrete, finite physical universe. Its main features are its being atomistic (no “atomless gunks”), hyper-extensional (identity of parthood entailing identity tout-court), and characterized by unrestricted mereological composition. Some basic notions of our universe, such as sequentiality, system, internal, external, are defined starting with the initial formal axioms.
Chapter 4 imports classical recursion theory into our model: given that our MoR are deterministic operators on discrete quantities, this is quite a natural move. After introducing some basic notions of function theory, such as the ones of partial and inverse operator, we show how positive integers can be represented as cell state configurations in our automaton, in a way analogue to their appearing as sequences of tallys in the tape of an ordinary Turing machine. Next, we show how such configurations of states, together with the dynamical rule animating our automaton, can provide physical realizers for (or, as philosophers say, “ramseyfy”) the basic functions of recursion theory, such as the zero function or the projection functions. More complex operators can then be defined starting with the basic ones via the standard recursive procedures. By importing in our framework the classic and well-known results of basic recursion theory, such interesting concepts as the notion of a meta-MoR, that is, of an operator taking as inputs the codes of other operators and simulating them, can be precisely defined.
The short Chapter 5 provides quick hints at possible algebraic developments of the theory, together with some considerations on the relevance of the notion of isomorphism, as applied to our theory of the MoR.
The Appendices point at some possible, and in our view interesting, extra- matematical developments of the theory. Appendix I includes some initial and tentative conjectures on the connections between our formal theory and computational linguistics. The framework, though, is classically logical and, indeed, model-theoretic. We believe that Montaguestyle grammar still is the best approach to computationally tractable semantics and, following such classic works as Chierchia-McConnell- Ginet’s Meaning and Grammar, we highlight its virtues.
Appendix II is an excursus on a promising technological spin-off: we highlight the connections between our computational model and some recent discoveries in the field of nanotechnology. As we explain there, researches have begun to show how such nanomaterials as graphene (one-atom thick layers of graphite with peculiar physical features) can actually implement cellular automata. We begin to show that the resulting physical implementation is strikingly similar to our cellular model.
Appendix III is an overview of the new and rapidly growing field of system biology: following Dennis Bray’s recent and wonderful book Wetware, we show how thinking of the physics and chemistry of living cells in terms of discrete implementation of deterministic operators, i.e., MoR, can provide interesting insights into the world of microbiology.
Finally, as non-native English speakers, we are very grateful to Camilla Peroni for smoothly translating and revising the original version of this book.
The possible applications of the mathematics of the models of reference are of major importance to us: as we begin to show in the book, it should not only recapture other kinds of mathematics, but also allow us to represent a possible model of the physical universe itself – a model that does not contradict our current, established experimental and scientific knowledge. It should also allow us to describe our mind’s cognitive activities, including those relating to such fields as creativity, intuition, and emotions.
We expect readers interested in computation in general to be puzzled by such a framework. However, if we provisionally assume that, at the bottom level of reality, “everything behaves alike”, our theoretical option might not look so bizarre. Mathematics is one of the most fascinating human enterprises, but from our viewpoint it is, first of all, the tool to understand the behavior of reality, as well as of our mind investigating reality – perhaps in order to win the prize of the endless extension of human life-span.
The Introduction of our book informally presents the theoretical pillars of our theory, to be developed in subsequent Chapters: the notion of Model of Reference (for which we will often use the abbreviation “MoR” for convenience, without distinction between singular and plural) which is – behind a somewhat unusual terminology – the general idea of a deterministic, algorithmic operator; and the discrete universe hypothesis, which we take from such classic – albeit non-standard – approaches to the physics of computation as Stephen Wolfram’s New Kind of Science, Konrad Zuse’s works, and the by now well-established theory of cellular automata.
In Chapter 1, we describe the cellular automaton developed in our lab. We explore some of its basic mathematical features, highlighting in particular the strong reversibility of its dynamic rule, i.e., the fact that not only distinct initial states in the evolution of the automaton lead to distinct final states, but also, any configuration of the automaton can be regained by running it backwards via the very same dynamic rule. Strong reversibility, as we explain there, is highly desirable both for theoretical and for practical reasons.
Next, we show how, by implementing such a rule, the automaton is capable of universal computation, i.e., it can simulate a universal Turing machine and compute (if Turing’s Thesis is right) anything computable, insofar as each cell of the automaton acts as a universal and reversible logical gate. The strategy we follow is the same as the one used by Berkelamp, Conway and Guy in their constructive proof that Conway’s celebrated cellular automaton, The Game of Life, is computation-universal: it consists in showing how all the basic building bricks of computation (memory, circuits, logical gates) can be emulated by patterns and configurations of (states of) the elementary cells of the automaton.
Chapter 2 introduces the formal symbolism used in the following: this is the canonical notation of first-order logic with identity and function symbols. The choice of the standard notation of elementary logic in a mathematical book is theoretically motivated: in the development of the book, the principles of our theory are introduced as non-logical, firstorder axioms that work as constraints on the admissible models, whereas the rules of first-order logic (the chosen form is classical natural deduction), being sound and complete, in principle allow one to infer all the axioms’ logical consequences.
Chapter 3 presents, in the form of a set of such axioms, the formal ontology underlying our automaton. This is a mereological framework describing a discrete, finite physical universe. Its main features are its being atomistic (no “atomless gunks”), hyper-extensional (identity of parthood entailing identity tout-court), and characterized by unrestricted mereological composition. Some basic notions of our universe, such as sequentiality, system, internal, external, are defined starting with the initial formal axioms.
Chapter 4 imports classical recursion theory into our model: given that our MoR are deterministic operators on discrete quantities, this is quite a natural move. After introducing some basic notions of function theory, such as the ones of partial and inverse operator, we show how positive integers can be represented as cell state configurations in our automaton, in a way analogue to their appearing as sequences of tallys in the tape of an ordinary Turing machine. Next, we show how such configurations of states, together with the dynamical rule animating our automaton, can provide physical realizers for (or, as philosophers say, “ramseyfy”) the basic functions of recursion theory, such as the zero function or the projection functions. More complex operators can then be defined starting with the basic ones via the standard recursive procedures. By importing in our framework the classic and well-known results of basic recursion theory, such interesting concepts as the notion of a meta-MoR, that is, of an operator taking as inputs the codes of other operators and simulating them, can be precisely defined.
The short Chapter 5 provides quick hints at possible algebraic developments of the theory, together with some considerations on the relevance of the notion of isomorphism, as applied to our theory of the MoR.
The Appendices point at some possible, and in our view interesting, extra- matematical developments of the theory. Appendix I includes some initial and tentative conjectures on the connections between our formal theory and computational linguistics. The framework, though, is classically logical and, indeed, model-theoretic. We believe that Montaguestyle grammar still is the best approach to computationally tractable semantics and, following such classic works as Chierchia-McConnell- Ginet’s Meaning and Grammar, we highlight its virtues.
Appendix II is an excursus on a promising technological spin-off: we highlight the connections between our computational model and some recent discoveries in the field of nanotechnology. As we explain there, researches have begun to show how such nanomaterials as graphene (one-atom thick layers of graphite with peculiar physical features) can actually implement cellular automata. We begin to show that the resulting physical implementation is strikingly similar to our cellular model.
Appendix III is an overview of the new and rapidly growing field of system biology: following Dennis Bray’s recent and wonderful book Wetware, we show how thinking of the physics and chemistry of living cells in terms of discrete implementation of deterministic operators, i.e., MoR, can provide interesting insights into the world of microbiology.
Finally, as non-native English speakers, we are very grateful to Camilla Peroni for smoothly translating and revising the original version of this book.
| A DISCRETE UNIVERSE | back to top |
|---|
 How is a universe in which matter and information are two sides of the same coin to be
conceived? Here’s the iLabs proposal. The universe (call it U) has to be discrete and finite, to
begin with, with minimal space-time units at its bottom (how minimal? 10-35 m for the
minimal space unit, and 10-44 seconds for the minimal time unit, might be good guesses, but
the exact sizes are irrelevant).
How is a universe in which matter and information are two sides of the same coin to be
conceived? Here’s the iLabs proposal. The universe (call it U) has to be discrete and finite, to
begin with, with minimal space-time units at its bottom (how minimal? 10-35 m for the
minimal space unit, and 10-44 seconds for the minimal time unit, might be good guesses, but
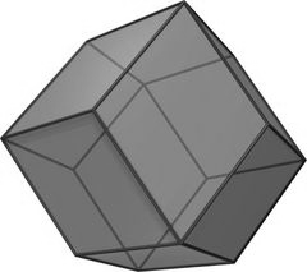
the exact sizes are irrelevant).We call these atoms cells. We expect the space to be entirely occupied by morphologically identical cells. So there exists a finite number w of cells, that is, of minimal space-time units. Likewise, time is divided into discrete minimal units, the instants: t0, t1, ... (speaking algebraically: time is a discrete linear order). Our intuitive, everyday Euclidean space is three-dimensional. But a discrete universe can be shaped for computational purposes in 1, 2, n dimensional spaces. To model our universe, we have chosen a two-dimensional, hexagonal grid (but our results can be obtained also by implementing our MsoR in a more traditional grid of squares, and in a threedimensional environment with the threedimensional analogue of hexagon: rhombic dodecahedron). Hexagon and rhombic dodecahedron have various topological advantages in the representation of physical movement – specifically, the distance between cells can be approximated in terms of radius:
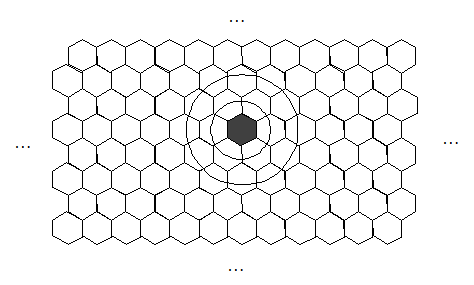
Once a spatial basis has been fixed, each cell in a bi-dimensional frame is univocally individuated as a point in a lattice by an ordered couple of integers, < i, j >. Next, at each instant t, each cell < i, j >instantiates exactly one state σ ∈ Σ , where Σ is a finite set of states of cardinality k. Let “σ i, j, t” denote the state of cell < i, j > at time t.
This is our strictly conventionalist perspective: first, we believe that the huge variety of worldly objects with their properties, qualities, and features surrounding us emerges as a high-level by-product of these simple ingredients: atomic cells and their few basic states. Second, anything whatsoever is ultimately an aggregate of cells. Call system any such aggregate. Then any system is just as legitimate as any other, our ordinary objects being just the aggregates that match with our ways of carving reality – and these depend on our cognitive apparatus, our learning capacities, and our practical interests.
The universe does not work randomly: rules determine how each point in the lattice updates its state. We don’t know what the basic rules are, but we know for sure that they have to be models of reference: deterministic sequences of inputs, elaborations, and outputs. Next, our bet is that, at the bottom, rules must be few and simple: complexity and variety should emerge at higher levels, and depend upon the underlying simplicity: simplex sigillum veri.
There are no mysterious “actions at a distance” in the universe, but just local interactions: each point < i, j > interacts only with the six adjacent cells, called its neighbourhood:
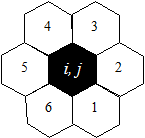
Let us label “[i, j]” point < i, j >’s neighborhood. Then, some deterministic dynamic MoR-rule governs the atoms – and thus, the world: at each instant t, each point < i, j > synchronically updates its state with respect to instant t-1, following the unique MoR φ:Σ→Σ, such that for each σ, < i, j >, and t :
σ i, j, t+1 = φ(σ [i, j], t)
Our world hosts a globally finite amount of information: given k and a number of w of points in the lattice, we have at most kw global configurations for U. Therefore, the entire evolution of our universe U is a finite global transition graph, GΦ - the graph of the global transition function Φ:Γ→Γ(with Γ the phase space or set of global configurations of U) induced by the MoR Φ.
| UNIVERSAL COMPUTATION | back to top |
|---|
The dynamical laws of physics are reversible at micro-level: distinct initial states in a
microphysical system always lead to distinct final states. It is likely that any formal model
aiming at capturing computations that actually go on down there, at the bottom of reality,
must host a reversible dynamics. On the other hand, irreversible computation is an impractical waste of energy. An AND gate
gives us 0 as its output at t+1. What was the input at t? 0 and 1, or vice versa, or two zeros? As von Neumann already conjectured, this informational entropy costs ~3 • 10-21 joules per
elementary computational step at room temperature. The loss of information has a
thermodynamic cost, to be paid in terms of a loss of non-computational energy. This does
not depend on inefficient circuit design: it follows directly from the existence of irreversible
calculation. As technology advances, this informational entropy problem is to put pressure
on us: we may need reversible computing devices sooner than we thought.
iLabs have developed a mathematical model (a finite state cellular automaton) displaying a erfectly reversible dynamics and capable of conserving the totality of the information stored at the beginning of the universe. Next, we have effectively proved that our automaton is capable of universal computation: our discrete, computational universe can host universal Turing machines, capable of computing (given Turing’s Thesis) anything which can be computed. This hinges on each single cell of our universe’s being capable of instantiating a single MoR as a computational primitive. Our model is thus a good candidate for the realization of high performance computational devices: systems capable of hosting logical circuits that perform computations with internal energy dissipation virtually close to zero.
iLabs have developed a mathematical model (a finite state cellular automaton) displaying a erfectly reversible dynamics and capable of conserving the totality of the information stored at the beginning of the universe. Next, we have effectively proved that our automaton is capable of universal computation: our discrete, computational universe can host universal Turing machines, capable of computing (given Turing’s Thesis) anything which can be computed. This hinges on each single cell of our universe’s being capable of instantiating a single MoR as a computational primitive. Our model is thus a good candidate for the realization of high performance computational devices: systems capable of hosting logical circuits that perform computations with internal energy dissipation virtually close to zero.
| FORMAL ONTOLOGY | back to top |
|---|
A model of the universe where the physical and informational reality are isomorphic is an ideal candidate to formally represents functions, algorithms, concepts and properties. Together with the standard formalism of cellular automata theory, iLabs developed a formal theory - a full-fledged ontology - to describe qualitatively objects and properties in the universe.
The mereological framework is intuitive and easy to grasp. A mereology is a theory that formally defines the notion, and so the MoR, parthood. Using this primitive notions other useful concepts can be introduced in the deductive machinery - atom, system, internal, external.
If MoR preserve their "fractal" nature at each and every scale - as we are inclined to conjecture - we believe that the approach can be generalized in order to represent countless objects, properties and events: this ontology is the first, necessary, step towards a completely computable knowledge database.
The mereological framework is intuitive and easy to grasp. A mereology is a theory that formally defines the notion, and so the MoR, parthood. Using this primitive notions other useful concepts can be introduced in the deductive machinery - atom, system, internal, external.
If MoR preserve their "fractal" nature at each and every scale - as we are inclined to conjecture - we believe that the approach can be generalized in order to represent countless objects, properties and events: this ontology is the first, necessary, step towards a completely computable knowledge database.
| RECURSIVE MODELS OF REFERENCE | back to top |
|---|
Intuitively, a recursive MoR is one that “refers to itself” in its very definition. Slightly more
precisely: a recursive MoR is such that its actions or outputs given certain perceptions or
inputs are determined by the output of that very MoR with respect to simpler inputs or
perceptions: what a recursive MoR does given some more complex perceptions depends on
what it does, or would do, for simpler ones (and, as shown in detail in our book, also
“simpler” can be characterized mathematically in a precise way). Recursive MsoR can
therefore be introduced via standard recursive definitions: the operator in the definiendum recurs in the definiens.
By fully recapturing the theory of recursive operators, the mathematics of the MsoR allowed iLabs to define the key notion of meta-model. Informally, a meta-model is simply a model of reference capable of perceiving other models of reference and of operating on them. Technically, this has been achieved by having MsoR themselves encoded as states of the cells inhabiting our digital universe U: a meta-model can then take as inputs the codes of the MsoR it perceives.
By embedding Kleene’s (Strong) Recursion Theorem in the theory of MsoR, it was then proved that there can be a universal MoR, capable of emulating the thoughts of any recursive MoR. This is a (partial) MoR with the following form:
univ(e, < x1, ..., xn>).
Given a recursive n-ary f(x1, ..., xn) with code e, that is [e]n(x1, ..., xn), univ takes as inputs the code of f and (the code for) its input, and provides as output the one f or [e]n would give:
f(x1, ..., xn) ≅ [e]n(x1, ..., xn) ≅ univ(e, < x1, ..., xn>).
univ obviously corresponds to a UTM and it can be implemented in our digital universe U.
By fully recapturing the theory of recursive operators, the mathematics of the MsoR allowed iLabs to define the key notion of meta-model. Informally, a meta-model is simply a model of reference capable of perceiving other models of reference and of operating on them. Technically, this has been achieved by having MsoR themselves encoded as states of the cells inhabiting our digital universe U: a meta-model can then take as inputs the codes of the MsoR it perceives.
By embedding Kleene’s (Strong) Recursion Theorem in the theory of MsoR, it was then proved that there can be a universal MoR, capable of emulating the thoughts of any recursive MoR. This is a (partial) MoR with the following form:
univ(e, < x1, ..., xn>).
Given a recursive n-ary f(x1, ..., xn) with code e, that is [e]n(x1, ..., xn), univ takes as inputs the code of f and (the code for) its input, and provides as output the one f or [e]n would give:
f(x1, ..., xn) ≅ [e]n(x1, ..., xn) ≅ univ(e, < x1, ..., xn>).
univ obviously corresponds to a UTM and it can be implemented in our digital universe U.
| RECURSIVE SELF-REFERENCE AND BEYOND | back to top |
|---|
Recursive self-reference takes place when a MoR not only refers to itself, but is aware of
such a self-reference. A system implementing a self-referentially recursive MoR can
therefore be aware of what it does via that very MoR.
Again, this is not semantic animism. For such expressions as “being aware” can be given a precise mathematical meaning. Much research at iLabs is guided by the persuasion that recursive self-reference is at the basis of what people ordinarily call “consciousness”: a key difference between conscious thoughts and any other computational procedure is that our mind, as (self-)conscious, can think about and have a viewpoint on itself (albeit with arguably limited powers to operate on its own source code). If Artificial Intelligence is to be real, this will be achieved by means of recursive self-reference – or this is our bet.
The Recursion Theorems, applied to our recursive MsoR, guarantee that we can define partial MsoR which are recursively self-referential, for they include their own code in their recursive definition. These are simply classical fixed-point definitions. Since numeric codes are perceptions taken as inputs by (meta-)models of reference, which can also emulate the thought procedures performed by the encoded MsoR, recursive selfreferential MsoR can perceive themselves in a precise mathematical fashion, and represent the computational procedure in which they consist within themselves.
Again, this is not semantic animism. For such expressions as “being aware” can be given a precise mathematical meaning. Much research at iLabs is guided by the persuasion that recursive self-reference is at the basis of what people ordinarily call “consciousness”: a key difference between conscious thoughts and any other computational procedure is that our mind, as (self-)conscious, can think about and have a viewpoint on itself (albeit with arguably limited powers to operate on its own source code). If Artificial Intelligence is to be real, this will be achieved by means of recursive self-reference – or this is our bet.
The Recursion Theorems, applied to our recursive MsoR, guarantee that we can define partial MsoR which are recursively self-referential, for they include their own code in their recursive definition. These are simply classical fixed-point definitions. Since numeric codes are perceptions taken as inputs by (meta-)models of reference, which can also emulate the thought procedures performed by the encoded MsoR, recursive selfreferential MsoR can perceive themselves in a precise mathematical fashion, and represent the computational procedure in which they consist within themselves.